Deep Q-Learning Network(DQN)
什么是Q-Learning
The Q comes from “the Quality” of that action at that state. Q-Learning是一种离策略(off-policy)的基于价值(value-based)的方法, 它使用时序差分(TD, Temporal Difference)方法来训练其动作价值函数。
Q函数使用Q表来存储每个状态-动作对的值。给定一个状态和动作,我们的Q函数会在Q表中查找并输出对应的值。
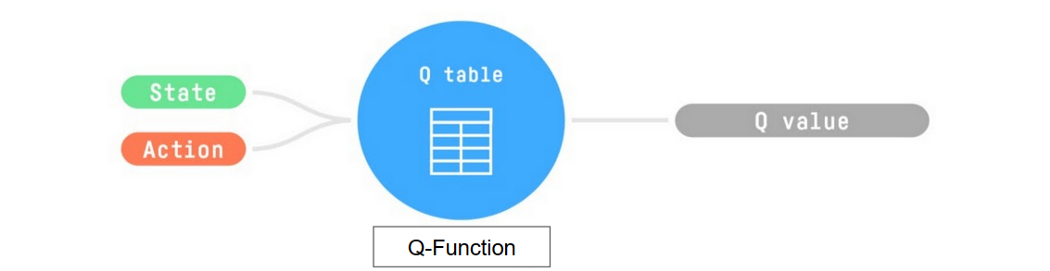
我们所需要的policy: 就是找出可以使Q值最大的Action
探索/利用
epsilon-贪心策略是一种处理探索/利用权衡的策略。
验证和为1:
其中:
- 是在状态s下选择动作a的概率
- 是探索率
- 是动作集的大小
- 是状态-动作值函数
这个想法是,从初始值ε = 1.0开始; 在训练开始时,由于ε非常高,进行探索的概率将会很大,所以大多数时候我们会探索。 但随着训练的进行,我们的Q表在估计方面变得越来越好,我们逐渐降低epsilon值, 因为我们需要的探索越来越少,而需要更多的利用。 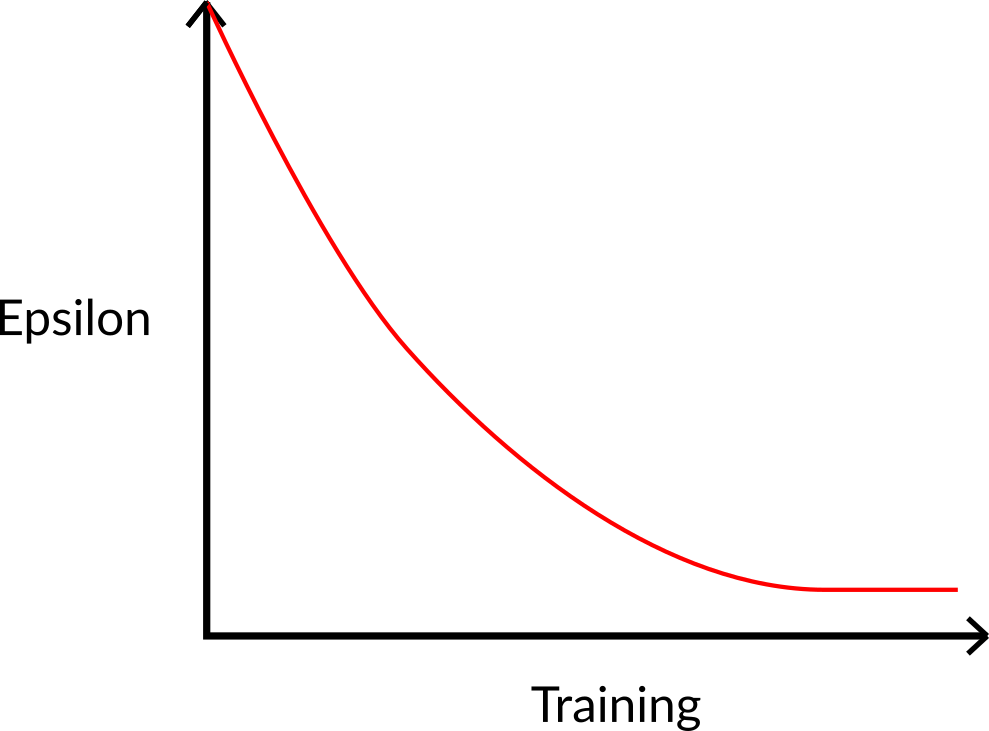
时序差分(TD, Temporal Difference)
为了得到我们的TD(时序差分)目标值,我们使用了即时奖励 Rt+1Rt+1 加上下一个状态的折扣值, 这个折扣值是通过在下一个状态找到使当前Q函数最大化的动作来计算的。 (我们称之为自举/引导估计)。
所以我们公式表示为下面形式
其中:
- α:学习率
- γ:折扣因子
From Q-Learning to Deep Q-Learning
问题在于Q-Learning是一个基于表格的方法。当状态和动作空间太大而无法用数组和表格有效表示时, 这就成为了一个问题。换句话说:它不具有可规模化的能力。 Q-Learning只在状态空间较小的环境中表现良好,比如:
- FrozenLake, we had 16 states.
- Taxi-v3, we had 500 states.
Atari 游戏环境的观察空间形状为 (210, 160, 3)*, 其中包含的值范围从 0 到 255,这给我们带来了 256^(210×160×3) = 256^100800 种可能的观察结果(相比之下,在可观测宇宙中大约有 10^80 个原子)。
Therefore, the state space is gigantic; due to this, creating and updating a Q-table for that environment would not be efficient. In this case, the best idea is to approximate the Q-values using a parametrized Q-function Qθ(s,a)Qθ(s,a) .
This neural network will approximate, given a state, the different Q-values for each possible action at that state. And that’s exactly what Deep Q-Learning does.
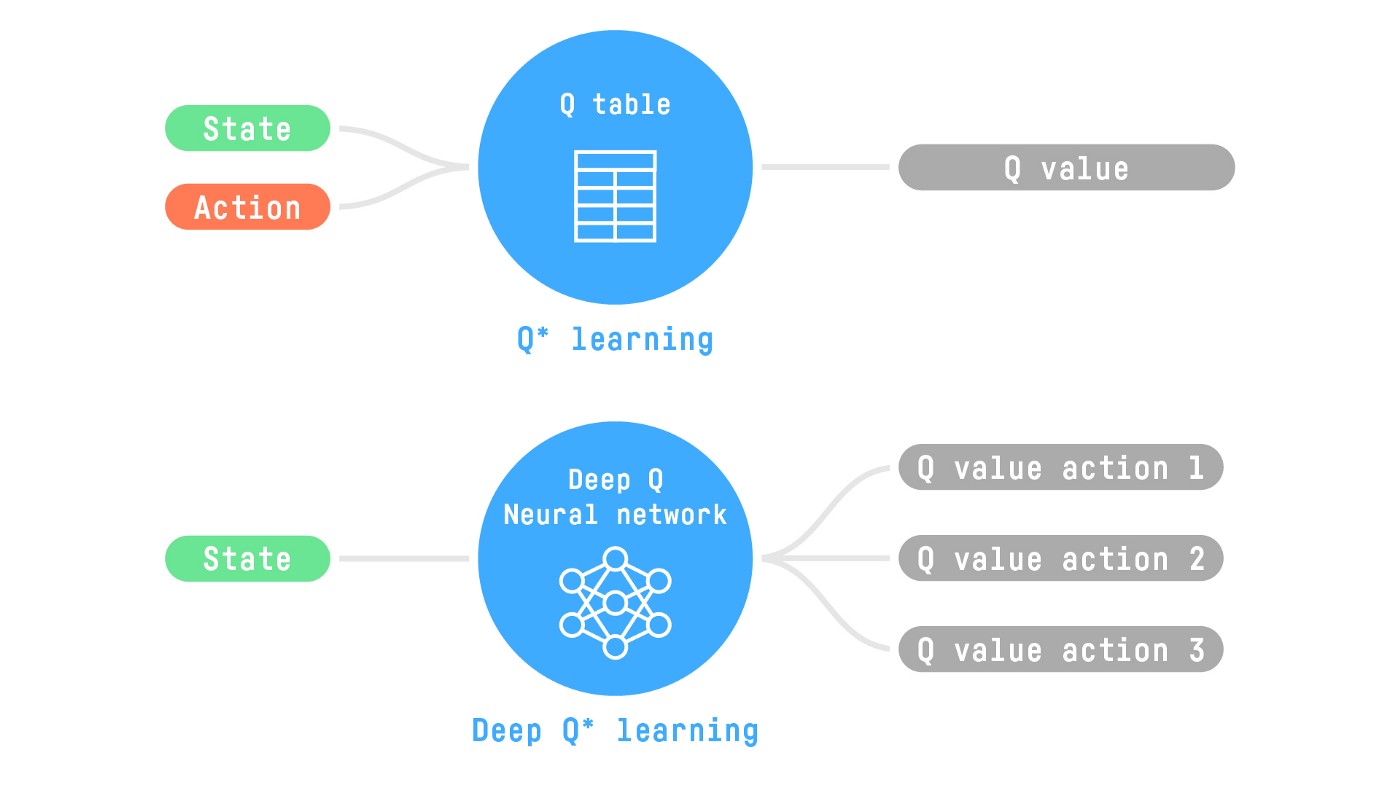
The Deep Q-Learning Algorithm
We learned that Deep Q-Learning uses a deep neural network to approximate the different Q-values for each possible action at a state (value-function estimation).
The difference is that, during the training phase, instead of updating the Q-value of a state-action pair directly as we have done with Q-Learning:
in Deep Q-Learning, we create a loss function that compares our Q-value prediction and the Q-target and uses gradient descent to update the weights of our Deep Q-Network to approximate our Q-values better.
Q-target
And this is translated into the following formula in DQN
